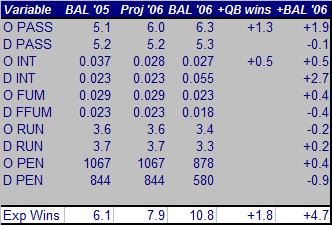
INTRODUCTION
Over the past few weeks, I've been interested in the amount of luck in NFL outcomes. I was interested primarily because I wanted to know just how good a game prediction model can get. In other words, what's the theoretical best that a prediction model can do? 70% correct? 95% correct? I think I've stumbled upon the answer.
The very best computer models predict winners at only a 70-75% rate. But that's not saying much because a monkey could predict winners 50% of the time. A monkey who knows which team is the home team could be correct 58% of the time. Even the Las Vegas odds makers aren't much better. They're correct less than 65% of the time.
It got me thinking. If a team is the very best team in the NFL, why wouldn't it have a 100% chance of winning each game? Why aren't there lots of 16-win teams? I thought that there must be good deal of luck involved to prevent the #1 team in the league from winning more than 13 or 14 games each year. Otherwise, why wouldn't the best team win 16 games every year?
In this post, I'll compare the actual distribution of NFL season wins to the distribution of a league determined by pure luck. Next, I'll compare the actual distribution to a league that theoretically is based on pure skill. Then finally, I'll show how I mathematically synthesized those two comparisons to determine exactly how much of the NFL is really just luck.
WHAT I MEAN BY LUCK
I'm not talking about a freak gust of wind or a slick patch of turf at a critical time and place to alter the outcome of a game. Although things like that happen, I'm talking about a much more ordinary phenomenon. An example I've used before goes like this:
Consider a very simple example game. Assume both PIT and CLE each get 12 1st downs in a game against each other. PIT's 1st downs come as 6 separate bunches of 2 consecutive 1st downs followed by a punt. CLE's 1st downs come as 2 bunches of 6 consecutive 1st downs resulting in 2 TDs. CLE's remaining drives are all 3-and-outs followed by a solid punt. Each team performed equally well, but the random "bunching" of successful events gave CLE a 14-0 shutout.
The bunching effect doesn't have to be that extreme to make the difference in a game, but it illustrates my point. Natural and normal phenomena can conspire to overcome the difference between skill, talent, ability, strategy, and everything else that makes one team "better" than another.
For more on how I define luck, see this post.
A PURE LUCK LEAGUE
What if the NFL was 100% luck? By that I mean, "what if the winner of each game was determined as if it were a flip of a fair coin?" The binomial distribution gives us the answer. The distribution mimics a bell-curve normal distribution. The graph below is a histogram of season win totals in a pure luck league.
As we'd expect, it illustrates that in such a league with 16 games, 8 wins would be the most common season outcome. About 20% of all teams would finish 8-8. About 5% of all teams would finish 11-5 and another 5% would finish 5-11. Almost no teams would finish undefeated or winless (each having a 0.00002 probability).
This type of league represents perfect parity. Every team has exactly a 50% chance of winning each game. To spectators (and NFL analysts) however, it would still appear that some teams are "better" than others. Some teams would even appear "hot" because they won several games in row, when in reality it's just an artifact of luck. (Sometimes when you flip a coin you get heads a few times in a row.) Does the coin have momentum? Is it hot? Some coins would have an above average number of heads several seasons in a row. Is that coin a dynasty?
But the real question is: How does the actual distribution of NFL regular season wins compare to the hypothetical luck league? How different is the observed distribution from an idealized distribution of pure luck? The histogram below shows the distribution of the actual NFL regular season win totals for every team since 2002, when the current division structure and scheduling system began. It's slightly irregular because it represents just five seasons (160 team records).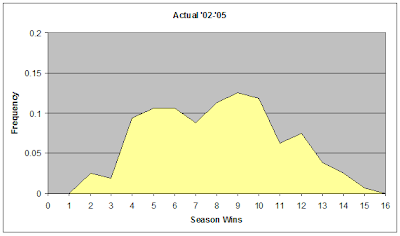
9-7 turns out to be the most common W-L record, followed by 10-6. I didn't expect that. At first, I thought I had discovered something interesting in the "dip" that the distribution takes at 7 wins. I thought that it was evidence that, even more often than we'd expect, teams with playoff hopes usually beat teams with nothing to gain at the end of the season. This effect would result in extra occurrences of 10-game winners. But after running many simulations of random sets of five seasons, irregularities like that were very common by chance alone. (More on that later.)
Let's compare the two distributions--pure luck vs. actual. The next histogram shows both distributions together, and at the same relative scale.
So how different are the distributions? Statistically, they are absolutely not similar. The goodness-of-fit test for two distributions is the chi-square test. It tells us it is infinitesimally unlikely that the actual distribution is sampled from the binomial distribution (p=8.9E-34). But that is obvious enough by just looking at them. To me, it looks like the actual distribution is a flattened version of the binomial distribution. It's as if something is "squashing" the luck distribution to create the actual distribution.
By comparing the two distributions, we can calculate that of the 160 season outcomes, only 78 of them differ from what we'd expect from a pure luck distribution. That's only 48%, which would suggest that in 52% of NFL games, luck is the deciding factor!
To me, that was too hard to accept. Frankly, I didn't buy it, so I kept at it. In part 2 of this article I'll re-attack the question from the opposite direction. I'll compare a theoretical "pure skill" league with the actual NFL win distributions. We'll see that it's skill that's "squashing" the luck into the actual distribution.